티스토리 뷰
https://www.acmicpc.net/problem/9095
9095번: 1, 2, 3 더하기
문제 정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다. 1+1+1+1 1+1+2 1+2+1 2+1+1 2+2 1+3 3+1 정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오. 입력 첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다. 출력 각
www.acmicpc.net
오늘은 전형적인 DP 문제를 푼다
사실 조건이 크지 않아 전체 탐색을 해도 상관 없지만
이런 문제로 DP 연습을 하기 딱 좋다.
먼저 복잡도부터..
|
문제에서 추출한 조건 1. 첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다. -> T의 범위가 없어 2. 정수 n이 주어졌을 때, n을 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오. -> 한 케이스에서 계산할 분기는 3개로 n depth 까지 전체 탐색할 경우 O(3^n) ... -> 여기서 정수 n 을 넘어가는 경우는 pruning 을 할거라 위 복잡도보단 낮을듯 |
여기서 n 이 주어졌을 때, 먼저 볼 수 있는 경우는 아래의 세가지 케이스가 나온다.
case1 -> 1 + (n-1)
case2 -> 2 + (n-2)
case3 -> 3 + (n-3)
아래와 같이 문제 예제 케이스로 보면 위 케이스로 나뉘어 질 수 있다.
예제의 case1 에서 보면 결국 1 + (3을 다시 1, 2, 3의 합으로 나타낸 수) 로 볼 수 있다.
|
정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다 case1 :
case2 :
case3 :
|
여기서 드는 생각은 다시 부분문제로 나뉘어 진다는 것이다.
※ DP (Dynamic Programming) 의 핵심 개념 참고
1. 전체 문제를 부분문제로 나눠서 풀기
2. 중복된 부분은 메모이제이션
DFS 풀이
n=3 일 경우 아래와 같은 케이스가 나온다. Leaf 노드에 해당하는 개수가 경우의 수라고 보면 된다.
아래 그림은 3을 1 + (2의 부분문제) , 2 + (1의 부분문제), 3 + (0의 부분문제) 로 나눈 것이고 아래도 그런 형태로 나눠져 내려간다고 생각하면 된다.

여기까지의 코드는 쉽다.
static int dfs(int n) {
if(n==0) return 1;
int case1 = 0;
int case2 = 0;
int case3 = 0;
if(n-1 >= 0) case1 = dfs(n-1);
if(n-2 >= 0) case2 = dfs(n-2);
if(n-3 >= 0) case3 = dfs(n-3);
return case1+case2+case3;
}
위와 같은 재귀형 코드가 나오게 된다.
DP 하향식 (TOP-DOWN) 풀이
여기서 눈치 챌 분들은 눈치를 챘겠지만, 중복되는 형태가 나오게 된다.
아래와 같이 4를 1, 2, 3의 합으로 나타낼 경우 위에서 본 n=3 일 경우의 부분문제와 동일한 형태의 분기가 탄생한다.
n=2 일때의 분기도 아래에서 보면 중복으로 보인다.
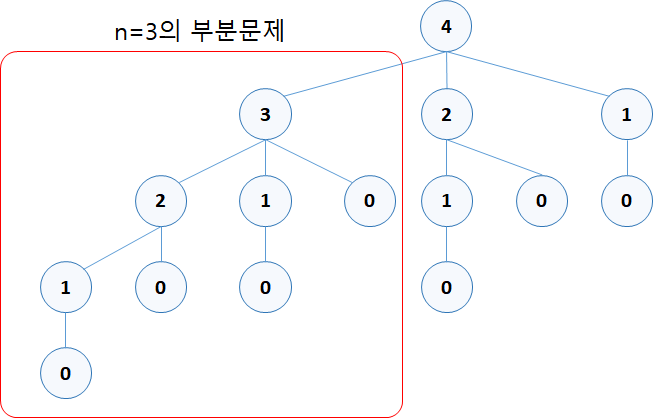
이처럼 중복으로 나오는 부분 문제는 메모이제이션을 통해
똑같은 input 값에 똑같은 output 값이 나오니까 한번 계산한 값을 그대로 가져다 쓰면 된다.
그럼 코드는 아래와 같이 된다.
return 문에서 계산한 값들을 선언해놓은 D라는 메모리에 저장해둔 후
분기에서 D[n] 값이 있는 경우는 밑에 분기를 탈 필요가 없이 계산해둔 값을 그대로 리턴한다.
static int dp(int n) {
if(n==0) return 1;
if(D[n] != 0) return D[n]; // 분기 탈 필요 없이 계산해둔 값 리턴
int case1 = 0;
int case2 = 0;
int case3 = 0;
if(n-1 >= 0) case1 = dp(n-1);
if(n-2 >= 0) case2 = dp(n-2);
if(n-3 >= 0) case3 = dp(n-3);
return D[n] = case1 + case2 + case3; // 부분문제를 통해 구한 값으로 메모이제이션
}
DP 상향식 (BOTTOM-UP) 풀이
DP가 어려운 이유 중 하나는 점화식을 세우는 것이다.
보통은 반복문을 통한 상향식 방식으로 접근하게 되는데,
그러다 보니 초기값은 무엇으로 할지 점화식이 어떤식으로 해야 할지 감이 오지 않을 것이다.
근데 위와 같이 풀다 보면 뭔가 눈치를 챌 수 있는데 return 문은 결국 아래와 같이 보여질 수 있다.
D[n] = dp(n-1) + dp(n-2) + dp(n-3) => D[n] = D[n-1] + D[n-2] + D[n-3]
점화식을 뽑아내는 방식은 위와 같은 훈련이 되어 있다면
분기는 어떤 방식으로 뽑힐 것이고, 부분문제로 결국 전체 문제를 풀어가야 하는 것을 볼 수 있다.
그래서 부분문제를 미리 풀어 놓고 (초기 값 세팅) , 점화식을 통해 최종 값에 도달 (전체 문제 해결) 하게 되는 것이다.
static int dp2(int n) {
D[0] = 1; // 초기 부분문제 해결
for(int i=1;i<=n;i++){
if(i-1 >= 0) D[i] += D[i-1];
if(i-2 >= 0) D[i] += D[i-2];
if(i-3 >= 0) D[i] += D[i-3];
}
return D[n];
}
코드에서 뭐 n=1, n=2, n=3 일때 미리 값을 풀어놓고 i=4 이상부터 처리할 수도 있다.
위처럼 부분문제를 어느정도 풀어놓고 전체 문제를 풀어가도록 한다.
보통은 Leaf 노드에 해당하는 값들이 초기값이 됨
main 코드
static final int MAX = 11;
static int T;
static int[] D;
//비용의 범위 조건에 따라 int나 long
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter (System.out));
T = Integer.parseInt(br.readLine());
for(int test_case=1;test_case<=T;test_case++){
int n = Integer.parseInt(br.readLine());
D = new int[n+1];
int Answer = dp2(n);
// int Answer = dp(n);
// int Answer = dfs(n);
bw.write(String.format("%d\n", Answer));
bw.flush();
}
bw.close();
br.close();
}위 풀이들을 이용해서 T 개의 값을 받아 매번 계산해서 출력해주는 코드다.
여기서 또..생각해보면 T에 대한 조건이 없으니 값을 찾는 최적화를 했어도 오래 걸리는거 아닐까?
여기서 n의 값이 11보다 작다고 되어있네. 11까지 풀어버림
상관 없고 값에 따라 항상 나오는 가지수가 같기 때문에 미리 D[1] ~ D[11] 까지 풀어버리고
Test Case에서 나오는 n에 따라 계산된 값만 출력해주면 된다!
static final int MAX = 11;
static int T;
static int[] D;
//비용의 범위 조건에 따라 int나 long
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter (System.out));
T = Integer.parseInt(br.readLine());
// n (1<=n<=11) 의 값에 따라 가지 수가 항상 같이 때문에
// D를 초기화 시킨 후 n의 입력만 받아 D[n]으로 출력하는 것이 최적화
D = new int[MAX+1];
D[0] = 1;
// 부분문제 해결
//부분문제 이용하여 큰 문제 해결
for(int i=1;i<=MAX;i++){
if(i-1 >= 0) D[i] += D[i-1];
if(i-2 >= 0) D[i] += D[i-2];
if(i-3 >= 0) D[i] += D[i-3];
}
for(int test_case=1;test_case<=T;test_case++){
int n = Integer.parseInt(br.readLine());
bw.write(String.format("%d\n", D[n]));
bw.flush();
}
bw.close();
br.close();
}
끗
DP는 참 재밌어
'Computer Science > 알고리즘' 카테고리의 다른 글
| [정올] 자리배치 (문제번호 : 2098) (0) | 2020.02.14 |
|---|---|
| [KOITP] 꽃 진열 (문제ID : IOI_1999_FLOWER) (2) | 2020.02.14 |
| [백준] 2048 (EASY) (문제번호 : 12100) (1) | 2020.01.07 |
| [백준] 구슬 탈출2 (문제번호 : 13460) (1) | 2020.01.06 |
| [DP] 비둘기집 원리 (1) | 2018.12.20 |
- Total
- Today
- Yesterday
- 암호화폐
- excel parsing
- Bitcoin
- 백준
- 비트코인
- white paper
- leetcode
- Blockchain
- 스프링
- gRPC
- SpringBoot
- Spring
- 알고리즘
- Redis
- 동적계획법
- CARDANO
- Vue.js
- vuejs
- 스프링 시큐리티
- DP
- 아키텍처
- architecture
- kubernetes
- 사토시 나가모토
- Nealford
- Bruteforce
- k8s
- Java
- 블록체인
- 카르다노
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
